Google Kickstart Round F 2020 Solutions: Part 2 (Painter’s Duel)

In this post, we are going to go through Painter’s Duel problem from Google Kickstart Round F 2020. It’s based on one of the most interesting concepts of Game theory. Ready to find out what it is? Then, let’s dive in!

Painter’s Duel – Problem Statement

A new art museum is about to open! It is a single-story building in the shape of a large equilateral triangle. That triangle is made up of many smaller identical equilateral-triangle-shaped rooms, and the side length of the museum is S times the side length of any one of the rooms. Each room has doors connecting it to all other rooms with which it shares a side (not just a vertex).

Each room is identified by two numbers: the row of the building it is in (counting from top to bottom, starting from 1), followed by its position within that row (counting from left to right, starting from 1). Here is an example of how the rooms are connected and labeled when S = 3:

Alma and Berthe are artists who are painting the rooms of the museum. Alma starts in the room (R_A, P_A), and Berthe starts in a different room (R_B, P_B). Each of them has already painted their starting room. C of the other rooms of the museum are under construction, and neither Alma nor Berthe is allowed to enter these rooms or paint them.

Alma and Berthe are having a friendly competition and playing a turn-based game, with Alma starting first. On a painter’s turn, if their current room is adjacent to at least one unpainted room that is not under construction, the painter must choose one of those rooms, move to it, and paint it. Otherwise, the painter cannot move and does nothing on their turn. Once both painters are unable to move, the game is over. The score of the game is the number of rooms painted by Alma minus the number of rooms painted by Berthe.

Both painters make optimal decisions, with Alma trying to maximize the score and Berthe trying to minimize the score. Given this, determine the best score Alma can guarantee for the game, regardless of what Berthe does.

Input

The first line of the input gives the number of test cases, T. T test cases follow. Each case begins with one line containing six integers S, R_A, P_A, R_B, P_B, and C. Respectively, these are the side length of the museum (as a multiple of the side length of a room), the row and position of Alma’s starting room, the row and position of Berthe’s starting room, and the number of rooms that are under construction. Then, there are C more lines. The i-th of these lines (counting starting from 1) contains two integers R_i and P_i, representing the row and position of the i-th room that is under construction.

Output

For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the best score that Alma can guarantee for the game, as described above.

Limits

Time limit: 40 seconds per test set.
Memory limit: 1GB.
0 ≤ C ≤ S² – 2.
1 ≤ R_A ≤ S.
1 ≤ P_A ≤ 2 × R_A – 1.
1 ≤ R_B ≤ S.
1 ≤ P_B ≤ 2 × R_B – 1.
(R_A, P_A) ≠ (R_B, P_B).
1 ≤ R_i ≤ S, for all i.
1 ≤ P_i ≤ 2 × R_i – 1, for all i.
(R_i, P_i) ≠ (R_A, P_A), for all i.
(R_i, P_i) ≠ (R_B, P_B), for all i.
Either R_i < R_i+1, or R_i = R_i+1 and P_i < P_i+1, for all i < C.

Test Set 1

T = 48.
S = 2.

Test Set 2

1 ≤ T ≤ 100.
2 ≤ S ≤ 6.

Sample

Input	Output
2 2 1 1 2 1 0 2 2 2 1 1 2 2 1 2 3	Case #1: 2 Case #2: 0

Solution:

As some of you might have already guessed, this problem is based on the Minimax algorithm of Game Theory.

Solving any problem involves asking yourself a set of intuitive questions and finding answers to them. Imagine yourself as the painter. The very first question that you need to ask yourself is: What are my moves?

It turns out that there can be at most 3 moves that can be made by any player. Have a look at the diagram given below.

Here, if the current location [i,j] is [2,2], then we can move to [1,1], [2,1] or [2,3] (represented in color red). In other words, if j is even, then we can move to [i-1,j-1], [i,j-1], [i,j+1].

Similarly, if the current location [i,j] is [3,3], then we can move to [3,2], [3,4] or [4,4] (represented in color blue). In other words, if j is odd, then we can move to [i+1,j+1], [i,j-1], [i,j+1].

Let’s try Brute Force solution with recursion. Now comes the interesting question, that is, How to construct the recurrence relation?

For every recursion function we need to know:

• Parameters of recursion
• Base Case
• Primary Recurrence relation

For this problem, the state will be dependent upon 3 parameters:-

• Current location of Alma (x1,y1)
• Current location of Berthe (x2,y2)
• Which player is currently playing (max or min)

This can be represented as T(x1,y1,x2,y2,ismax).

Now comes the base case of recursion. This can be easily found out from the question, which says that “Once both painters are unable to move, the game is over“. So we need to first calculate the moves that can be made by both the Players irrespective of whether the current player is maximizing or minimizing. If there are no more moves to be made, then function will simply return 0.

Here comes the main question. How do we construct the recurrence relation?

We have two adversaries, one is trying to maximize and other is trying to minimize the total score. Our recurrence relation needs to model this fact. Let’s look at how we can go about it.

If the current player is Alma, then she will contribute +1 to the score and try out all her moves. The best move that will maximize the total score will be chosen. Next turn will be played by minimizer.

Let’s say, m is the list of all moves that can be made if the player is Alma. Then Recurrence function will look like:

T(x1,y1,x2,y2,1) = max( T(x1,y1,x2,y2,1), 1 + T(mx_i, my_i, x2, y2,0) ), if m is non-empty

T(x1,y1,x2,y2,1) = T(x1, x2, x2, y2,0) , otherwise

If the current player is Berthe, then she will contribute -1 to the score and try out all her moves. The best move that will minimize the total score will then be chosen. Next turn will be played by maximizer.

Let’s say, m is the list of all moves that can be made if the player is Berthe. Recurrence function can be given as:

T(x1,y1,x2,y2,0) = min( T(x1,y1,x2,y2,0), -1 +T(x1, y1,mx_i, my_i, 1) ), if m is non-empty

T(x1,y1,x2,y2,0) = T(x1, x2, x2, y2,1) , otherwise

We will also have to maintain a dictionary (visited), so that moves already made wouldn’t be chosen again by the players. For every move that is to be tried out, visited will be set as 1 and after trying out this move, it will be reset to 0. This is how we will backtrack.

def solution(arr,s,x1,y1,x2,y2,n):
  res=0
  visited={}
  for i in range(1,s+1):
    for j in range(1,2*i):
      visited[(i,j)]=0

  for i,j in arr:
    visited[(i,j)]=1

  #Initially both players have already painted their starting rooms
  visited[(x1,y1)]=1
  visited[(x2,y2)]=1

  #To calculate the moves that can be made by any player
  def calc_moves(i,j):
    moves=[]
    if j>1 and not visited[(i,j-1)]:
      moves.append([i,j-1])
    if j+1<2*i and not visited[(i,j+1)]:
      moves.append([i,j+1])
    if j%2==0 and i>1 and j>1 and not visited[(i-1,j-1)]:
      moves.append([i-1,j-1])
    if j%2!=0 and i+1<=s and not visited[(i+1,j+1)]:
      moves.append([i+1,j+1])
    return moves

  def dfs(x1,y1,x2,y2,ismax):   
    movesA=calc_moves(x1,y1)
    movesB=calc_moves(x2,y2)

    if not len(movesA) and not len(movesB):
      return 0

    besta,bestb=float('-inf'),float('inf')
    if ismax:
      if not len(movesA): #Simply, Give the chance to other player
        return dfs(x1,y1,x2,y2,0) 

      for i,j in movesA:
        visited[(i,j)]=1 #Try this move
        besta=max(besta,1+dfs(i,j,x2,y2,0))
        visited[(i,j)]=0 #Backtrack
      return besta

    else:
      if not len(movesB): #Simply, Give the chance to other player
        return dfs(x1,y1,x2,y2,1)

      for i,j in movesB:
        visited[(i,j)]=1 #Try this move
        bestb=min(bestb,-1+dfs(x1,y1,i,j,1))
        visited[(i,j)]=0 #Backtrack

      return bestb

  return dfs(x1,y1,x2,y2,1)

tests=int(input())
# One by one run for all input test cases 
for t in range(tests):
  s,x1,y1,x2,y2,n=list(map(int, input().split()))
  arr=[]
  for _ in range(n):
	  arr.append(list(map(int, input().split())))
  print("Case #{}: {}".format((t+1),solution(arr,s,x1,y1,x2,y2,n)))

Here, S can be at the most 6, as defined in the limits of Test Set 2. As we won't have many states, our Brute Force solution will work without any further optimizations.

Time Complexity: O(2^S2)

How many branches can the recurrence function take?

This can be a bit tricky. Most of you may say 3 as there can a maximum of 3 rooms that the painter can choose to go to.

But the correct answer is 2 rooms/branches.

This is because, 3 rooms can be selected only when each player is at its starting position. After that, at the most 2 rooms will be available, as the player must have already painted that third room.

Now what about the maximum depth of recursion?

This will be equivalent to total number of rooms in the equilateral museum. At each level i, we will have (2*i-1) rooms. For example, 3rd level from top has 2*3-1=5 rooms. So the total number of rooms for all levels will be 1+3+....+2*S-1.

This is an Arithmetic Progression given as:

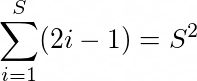
So the total time complexity comes out to be O(2^S2).

Space Complexity: O(S²)

Only S² space will be consumed for maintaining the visited dictionary and the maximum size of the recursion stack.

Want some more fun? Then go check out the Google Kickstart Round F Solutions to other problems at:

• Google Kickstart Round F 2020 Solutions: Part 1 (ATM Queue & Metal Harvest)
• Google Kickstart Round F 2020 Solutions: Part 3 (Yeetzhee)