Google Kickstart Round F 2020 Solutions: Part 3 (Yeetzhee)

In this post, we are going to go through Yeetzhee from Google Kickstart Round F 2020. This big brother of all problems is based on probability theory.

Before reading this, it is imperative that you should know the basics of what Expected value is and its important properties. Not sure what am talking about? Then check out my this post here. Let’s get started!

Yeetzhee – Problem Statement

Pommel is very bored at home so she has invented a new game involving N dice. Each die has the numbers from 1 to M written on it. Whenever she throws a die, it has an equal probability of landing on each of the M possible values.

Pommel places all the dice in a row. She goes through the dice one at a time from left to right. For each die she rolls, Pommel can either keep the value she rolled and move on to the next die or she can re-roll the die. Pommel can re-roll a die as much as she wants before moving on to the next die.

Once Pommel has gone through all the dice, the game is finished. To determine if she has won, she puts the dice into groups. All dice with the same value are put into the same group. So if she finishes the game with x distinct values, then there will be x groups. These groups of dice are then sorted by number of dice in non-decreasing order.

For example:

• If the final dice results are [2, 2, 3, 2, 2, 3], the dice would be put into two groups and ordered as follows: [3, 3] and [2, 2, 2, 2].
• If the final dice results are [1, 6, 7, 7], the dice would be put into three groups and ordered as follows: [6], [1], and [7, 7] (or equivalently, [1], [6] and [7, 7]).

Pommel wins if she finishes the game with exactly K groups, and the i-th group contains exactly A_i dice, for all i.

What is the expected value of the total number of dice rolls it will take Pommel to win the game, assuming she plays optimally to minimize this expected value?

It is guaranteed that for any valid input, it is possible for Pommel to win the game.

Input

The first line of the input gives the number of test cases, T. T test cases follow. The first line of each test case contains the integers N, M and K. Then, K lines follow describing the groups she must finish with. The i-th line contains A_i.

Output

For each test case, output one line containing Case #x: y, where x is the test case number (starting from 1) and y is the expected number of times it will take to roll all the dice for Pommel to win the game.

y will be considered correct if it is within an absolute or relative error of 10^-6 of the correct answer.

Limits

Time limit: 20 seconds per test set.
Memory limit: 1GB.
1 ≤ T ≤ 100.
1 ≤ K ≤ M.
1 ≤ A_i, for all i.
A₁ + A₂ + … + A_K = N.
A_i ≤ A_i+1, for all i.

Test Set 1

2 ≤ N ≤ 6.
2 ≤ M ≤ 6.

Test Set 2

2 ≤ N ≤ 50.
2 ≤ M ≤ 50.

Sample

Input	Output
2 3 6 2 1 2 5 2 1 5	Case #1: 4.7 Case #2: 9.0

Solution

Looking at the problem statement, many of you might have thought “Let’s skip!” right away after seeing that word ‘expected value’. But I promise that it isn’t as hard as it sounds. In fact if you see the answer, you’ll find that it’s hardly 25 lines of code if we exclude input preprocessing.

Now we can easily infer that there will be recursion involved in solving this problem. But the first question arises, What will be its state?

Obviously the state should be representative of the current dice configuration.

For N=3, M=6, K=2, let’s say we want 1 dice in first group and 2 in the second. So if the numbers on each dice are [1,1,2], [1,2,2], [2,3,3] and so on. All these will be winning configurations. This means that it doesn’t matter what we get on each dice. What matters is that the total number of dice in each of the K groups should be same as what we require.

From this we can conclude that the State of Recursion will be a tuple of length M, showing what number is present on how many dice.

That is, if some state is (0,0,0,0,1,1), then there will be 1 die in each of the 2 groups. The winning state will be the state having total count of dice in all groups equal to N.

You may ask that why not take a tuple of length K as there are K groups. The reason is, we want to calculate probability of die landing on each number here, so want all the M numbers to be present even though only K of them will be filled.

Okay we got the state. Now what’s the expected number of rolls to reach the winning state?

To understand this, let’s first unravel the Test Case 1, then we will dig deeper into the main concept of the problem.

Test Case 1:

We have N=3 dice, each having 1 to M=6 numbers written on them. We will win if we can manage to get K=2 groups of dice, one with 1 die and the other with 2 dice.

Let’s throw the first die. Here we can get any number from 1 to 6, that is, there are 6 possible ways, each with equal probability of 1/6.

Result so far=6*(1/6)=1 roll.

Let’s say we got a 1 on the first die. Now we’ll throw the second die. There will be 2 cases here:

• Second die matches the first. That means we got another 1!. There is just 1 way of getting 1. State = [0,0,0,0,0,2].
• Second die is different. That means anything other than 1. This can be achieved in 5 ways (2,3,4,5,6). State = [0,0,0,0,1,1].

As you can see, both the states are valid subsets of the winning state, that means, we can still choose all the numbers with equal probability. So there is no need to reroll.

Now the result will be 1+1=2.

Now for the third die, in order to win, we need to reach the state [0,0,0,0,1,2]. This can be achieved in 2 ways:

Case A: If the first and second dice are same.

Probability of this happening=1/6. Now, if we want to win then the third die needs to be different. We can do this in 6-1=5 ways out of 6 ways, that is, p=5/6.

So the average rerolls = (1/p) =6/5 = 1.2

Pray do tell me how we got the number of rerolls as (1/p)?

We can intuitively infer that if it takes probability p for a die to land on a good state, then the average number of rerolls that we will have to do is at the most (1/p)

Thus, Expected rolls = (average rerolls) * (Probability that first and second dice are same) = (6/5)*(1/6) = 0.2

Case B: If the first and second dice are different.

Probability of this happening=5/6. Now the third die should match either the first or the second die. We can do this in 2 out of 6 ways. p = 2/6 =1/3.

So the average rerolls = (1/p) =3

Expected rolls = (average rerolls) * (Probability that first and second dice are different) = 3*(5/6) = 2.5

Final result now becomes 1+1+0.2+2.5 = 4.7

Recursion:

Now let’s ask ourselves some very intuitive questions to construct the complete recurrence function.

What’s the final winning state?

This can be obtained by simple inserting (M – K) zeros to the beginning of the input list A to make the target of length M.

What’s the base case?

When we reach the final winning state, then we don’t have to make any further moves. Or rather we can simply say that when total count of dice for all the numbers in the state is equal to N, return 0.

This is because, we will only consider valid subsets of the winning state. For instance, if winning state = [0,0,0,0,1,2] then states like [0,0,1,1,0,0], [1,0,0,0,1,0] would be invalid. Valid states can be [0,0,0,0,1,0], [0,0,0,0,1,1], [0,0,0,0,0,2] and so on.

Last but not the least, What’s out recurrence relation?

Here comes the most important concept ‘Markov chain‘ on which this problem is based.

Markov Chains: Future Depends on Present and not Past!

A Markov chain can be used to easily represent highly complex real world systems with arbitrary states and transitions. These transitions, called as steps, can be modeled in the form of a transition matrix.

Markov chain is a mathematical process consisting of a serious of events wherein the probability of next event is only dependent upon the where the process is at present.

We are going to use this property of Markov Chain to form our recurrence relation. Let’s see how!

Consider Test Case 1 which has winning state = [0,0,0,0,1,2]. Suppose we are currently at state [0,0,0,0,0,1] and we want to find the expected number of rolls at this state, E([0,0,0,0,0,1]). We have already rolled a die and it has landed on, let’s say, index 5. We have 2 possibilities here, as already discussed:-

Next die roll can be different from the number on first die and thus land on any Index from 0 to 4.

We have a bunch of zeros from 0 to 4 index, so our dice can ideally roll on any of these. So from here we can go to state [0,0,0,0,1,1] in 5 ways. This is represented by variable ‘cnt‘ in our code.

OR the next die that we roll can match what we got on the first die and thus land on Index 5.

We have a single 1 at the 5^th index, so our die can roll on just that index. So from here we can go to state [0,0,0,0,0,2] in just 1 way.

If we look at both these cases, we can infer that our die can still land on any of the 6 numbers (6 ways) to reach the winning state. In our code, the variable ‘total’ represents this.

Using Markov chains, we can find E([0,0,0,0,0,1]) as follows:

E([0,0,0,0,0,1]) = (Average Rerolls at [0,0,0,0,0,1]) + (5/total)*E([0,0,0,0,1,1]) + (1/total)*E([0,0,0,0,0,2])

Average Rerolls at [0,0,0,0,0,1] = M/total = 6/6 = 1

Recurrence relation is :

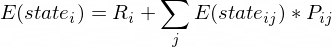
P_ij is the probability of reaching state j from state i. In our code this is:-

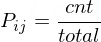
Here R_i will be the average number of rerolls at the current state.

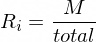
Further Optimizations:

We can use memoization to store the results of each state to further improve the time complexity of our problem.

Code:

Time Complexity:

Maximum depth of recursion will be equivalent to the total number of states of recursion, that is, Number of subsets of Winning State, let’s say S.

Also in each state, we are doing O(M) work. So the total time complexity would be O(M*S).

Space Complexity:

Size of the cache for memoization will be the total number of states of recursion equal to O(S). And maximum size of the recursion stack will also be equal to O(S).

So space complexity will be O(S), where S is the total number of subsets of winning state.

Fun Fact: Markov Chains are the basis for Page Rank algorithm. It is one of the most popular and the first ever algorithm developed by Google to rank different web pages in search results.

Want some more fun? Then go check out the Google Kickstart Round F Solutions to other problems at:

• Google Kickstart Round F 2020 Solutions: Part 1 (ATM Queue & Metal Harvest)
• Google Kickstart Round F 2020 Solutions: Part 2 (Painter’s Duel)